First Order Linear System
First order linear system. Systems of linear first-order odes Lecture 39 Differential Equations for Engineers - YouTube. Where P and Q are functions of xThe method for solving such equations is similar to. So the step signal is widely used in the time domain for analyzing the control systems from their responses.
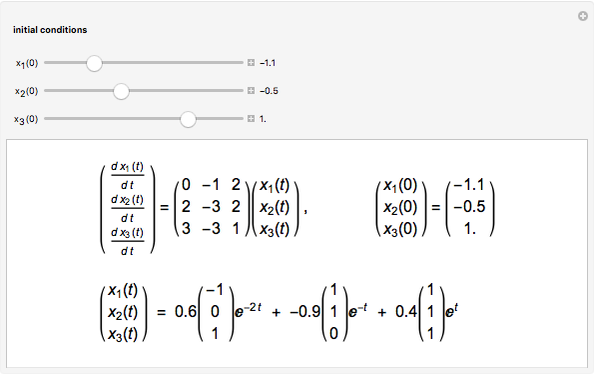
Finding the eigenspaces for lambda 1 we have. Those systems of two equations and two unknowns only. If the constant-coefficient first-order linear system of ODEs is written in the matrix form X A X b where X X t is the vector of unknown functions X X is the vector of derivatives of the unknown functions is the coefficient matrix and b is the non-homogeneous forcing vector the solution can be constructed from the eigenvalues and eigenvectors eigenpairs of the matrix.
Which is called a homogeneous equation. The linear first order system of equations becomes x0t Atxt. 1 is the same for all system variables.
Frequency and time responses. We invent two new functions of x call them u and v and say that yuv. Example The linear system x0 1t costx t sintx.
Thus a first order linear system is one that can be written in the form x Atx bt. We refer to a system of the form given in 3 simply as a linearsystemWe assume that the coefficientsaij as well as the functions fi are continuous on a common interval IWhen fit 0 i 1 2 n the linear system 3 is said to be homogeneousotherwise it is nonhomogeneous. Specifically it will help to get the matrix exponential.
Dx n dt F nx 1x nt. Well shorten this to first order linear system or even linear system. To solve the homogeneous system we will need a fundamental matrix.
Solving a Linear System by Elimination Definition.
Solving a Linear System by Elimination Definition.
Higher-order systems A more detailed course description. A first order linear system of ODEs is a system that can be written as the vector equation vec x t Pt vec x t vec f t where Pt is a matrix valued function and vec x. Dy dx P xy Q x Where P x and Q x are functions of x. Thus a first order linear system is one that can be written in the form x Atx bt. A system of n linear first order differential equations in n unknowns an n n system of linear equations has the general form. Well shorten this to first order linear system or even linear system. And if 𝑎0 0 it is a variable separated ODE and can easily be solved by integration thus in this chapter 𝑎0 cannot be 0. Dy dt y 0 9 and generates the characteristic equation. A first order differential equation is linear when it can be made to look like this.
A first order differential equation is linear when it can be made to look like this. If the constant-coefficient first-order linear system of ODEs is written in the matrix form X A X b where X X t is the vector of unknown functions X X is the vector of derivatives of the unknown functions is the coefficient matrix and b is the non-homogeneous forcing vector the solution can be constructed from the eigenvalues and eigenvectors eigenpairs of the matrix. A first order differential equation is linear when it can be made to look like this. Linear first order IVP systems always have unique solutions if At and. Here At is a matrix whose entries depend only on t and bt is a column vector whose entries depend only on t. Such a system is usually referred to as an n n first order system. Dx n dt F nx 1x nt.















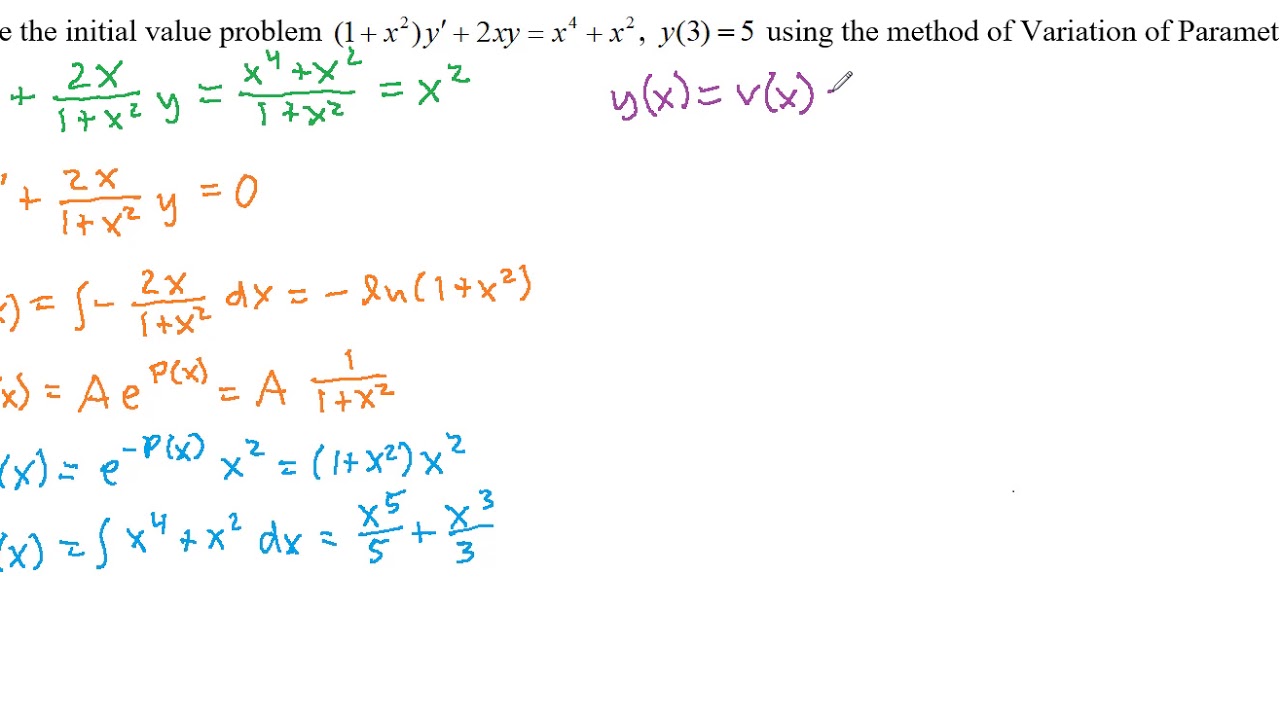





























Post a Comment for "First Order Linear System"